Abstract
Nuclear structure and mechanics are gaining recognition as important factors that affect gene expression, development, and differentiation in normal function and disease, yet the physical mechanisms that govern nuclear mechanical stability remain unclear. Here we examined the physical properties of the cell nucleus by imaging fluorescently labeled components of the inner nucleus (chromatin and nucleoli) and the nuclear envelope (lamins and membranes) in nuclei deformed by micropipette aspiration (confocal imaged microdeformation). We investigated nuclei, both isolated and in intact, living cells, and found that nuclear volume significantly decreased by 60–70% during aspiration. While nuclear membranes exhibited blebbing and fluid characteristics during aspiration, the nuclear lamina exhibited behavior of a solid-elastic shell. Under large deformations of GFP-lamin A-labeled nuclei, we observed a decay of fluorescence intensity into the tip of the deformed tongue that we interpreted in terms of nonlinear, two-dimensional elasticity theory. Here we applied this method to study nuclear envelope stability in disease and found that mouse embryo fibroblasts lacking the inner nuclear membrane protein, emerin, had a significantly decreased ratio of the area expansion to shear moduli (K/μ) compared to wild-type cells (2.1 ± 0.2 versus 5.1 ± 1.3). These data suggest that altered nuclear envelope elasticity caused by loss of emerin could contribute to increased nuclear fragility in Emery-Dreifuss muscular dystrophy patients with mutations in the emerin gene. Based on our experimental results and theoretical considerations, we present a model describing how the nucleus is stabilized in the pipette. Such a model is essential for interpreting the results of any micropipette study of the nucleus and porous materials in general.
INTRODUCTION
Central to eukaryotic cells, the nucleus contains genetic material and transcriptional machinery. The nucleus is delimited by the nuclear envelope, a highly specialized biological interface composed of two lipid membranes in which nuclear pore complexes (NPCs) are embedded. Underlying the inner nuclear membrane is a protein meshwork, the nuclear lamina, which consists largely of nuclear lamin proteins that are crucial for structural support of the nucleus (1,2). Lamins interact with both inner nuclear membrane proteins and chromatin (3,4). In addition to chromatin, the inner nucleus also contains subnuclear bodies that each associate with a distinct subset of protein and nucleic acid components for specific biological activity. Despite the importance of nuclear architecture for biological function, our knowledge of the physical mechanisms regulating nuclear structure and stability is not yet complete. This is critical for understanding how the nucleus senses and responds to physical forces.
A deeper comprehension of nuclear mechanics is also motivated by an increasing number of tissue-specific disorders that are linked to mutations in genes encoding lamins and associated nuclear envelope proteins. These disorders include Emery-Dreifuss muscular dystrophy, dilated cardiomyopathy, familial partial lipodystrophy, and Hutchinson-Gilford progeria syndrome (4–6). The pathogenic mechanism underlying these diseases remains unclear but it has been suggested that 1), mutations in genes encoding nuclear envelope proteins leads to altered gene expression; and 2), structural changes in the nuclear envelope compromise its mechanical stability, resulting in disruption of nuclear organization in tissues subject to repetitive strain. These two hypotheses are not mutually exclusive, and deciphering the role of nuclear mechanics in disease demands a better understanding of nuclear physical properties.
The structural stability of the inner nucleus and nuclear envelope can be probed by techniques including cell compression (2,7), cell strain (1,8,9), and micropipette aspiration. Previous micropipette studies have investigated the bulk properties and rheology of isolated nuclei (10–12) and we previously reported on nuclear envelope elastic properties in both living cells and isolated nuclei (13). Here we used micropipette aspiration together with bright-field microscopy and confocal imaging (confocal imaged microdeformation, CIMD) to reveal details about the physical properties of the inner nucleus and nuclear envelope components in living cells and isolated nuclei. During aspiration, we show that the nucleus decreases in volume by 60–70% and nuclear membranes bleb into the pipette, indicating flow through the nucleus. To investigate the role of nuclear envelope stability, we analyzed large, local deformations of the GFP-Lamin A-labeled (GFP-LamA) nuclear envelope in intact, living mouse embryo fibroblasts (MEFs) and interpreted GFP-LamA intensity profiles in terms of nonlinear, two-dimensional elasticity theory (13). Applying this method to cells deficient in emerin, a nuclear envelope protein implicated in Emery-Dreifuss muscular dystrophy (EDMD), we show that the nuclear envelope in both emerin-deficient and wild-type MEFs exhibited behavior of a continuous, two-dimensional elastic material. However, the ratio of the area expansion to shear moduli, K/μ, an important signature of the nuclear envelope's mechanical properties, was a factor of 2.5 less in emerin-deficient cells. Together our experimental observations provide the basis for a new model to describe nuclear shape stability under micropipette aspiration and validate the use of the technique for characterizing nuclear envelope mechanical stability in disease.
EXPERIMENTAL METHODS
Cell culture and materials
Emerin-deficient mouse embryo fibroblasts (MEFs) as well as wild-type controls were immortalized by repeated passage and were kindly provided by C. L. Stewart and S. Kozlov, National Cancer Institute, Bethesda, MD (14). HeLa cells were obtained from American Tissue Cell Culture (ATCC, Manassas, VA). Both HeLa and MEF cells were maintained at 37°C and 5% CO2 in Dulbecco's Modified Eagle Medium containing 10% fetal bovine serum, 1% glutamine, and 1% penicillin/streptomycin (BioWhittaker, Cambrex, East Rutherford, NJ).
Experiments were performed on intact MEF and HeLa cells, as well as on isolated HeLa cell nuclei. A procedure to isolate nuclei was developed from a previously described protocol (15). When the cells had attained ∼90% confluency, they were harvested by trypsinization, washed 3× with PBS and resuspended in a buffer of 10 mM HEPES-KOH (pH 7.9), 10 mM KCl, and 1.5 mM MgCl2 containing protease inhibitors (complete tablets, EDTA-free, Roche, Penzburg, Germany). Thereafter cells were incubated on ice for 5–10 min or until the plasma membranes were sufficiently swollen as observed by phase contrast microscopy. Dounce homogenization (typically 10 strokes of the tight pestle in a 7 mL Dounce tissue homogenizer (Wheaton Scientific Products, Millville, NJ)) released the nuclei that were then collected by centrifugation (1000 × g) for 5 min. After isolation, nuclei were resuspended in a physiological buffer formulated to reproduce ionic conditions in the cytoplasm (16): 130 mM KCl, 1.5 mM MgCl2, 10 mM Na2HPO4, 1 mM Na2ATP, and 1 mM DTT, pH 7.4. For ATP regeneration, 5 mM creatine phosphate and 0.1 mg/mL creatine phosphokinase were added.
The enhanced green fluorescent protein conjugated to Lamin A (GFP-LamA) construct was a generous gift from D. K. Shumaker and R. D. Goldman, Northwestern University, Chicago, IL (17). Transfection was performed with twofold excess carrier DNA (Herring testes DNA, Clontech, San Jose, CA) into HeLa/MEF cells at 70–80% confluency using CaPO4 (Invitrogen, Carlsbad, CA). The GFP-LamA delineated lamina was visualized in living MEF and HeLa cells as well as in isolated HeLa cell nuclei. Membranes of isolated nuclei were labeled by incubation with 1,1′-dioctadecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (DiIC18, Molecular Probes, Eugene, OR) at a final concentration of 0.01 μM in physiological buffer for 15 min. Nuclei that were not cleanly isolated and remained associated with external membranes from, for example, the endoplasmic reticulum, were easily identified as the membrane staining extended beyond the periphery of the nucleus itself and were excluded from the analysis. SYTOX Orange Nucleic Acid Stain (Molecular Probes, Eugene, OR) was used to stain nucleic acids by incubation with isolated nuclei at a final concentration of 0.1 μM before imaging. The nuclear interior and nucleoli were visualized in living HeLa cells transfected with CFP-NLS-NLS-NLS (Clontech, San Jose, CA) using the same transfection protocol as described above. CFP-NLS-NLS-NLS (CFP-NLS×3) consists of an eCFP fluorophore fused to three consecutive nuclear localization sequences (NLS). The NLS targets proteins to the nucleus (18), and three consecutive NLS sequences are thought to preferentially localize the protein to nucleoli (J. S. Andersen, 2005, personal communication). CFP-NLS×3 has no known specific interactions with nuclear structures.
Bright-field micropipette aspiration
Micropipette aspiration was used to deform nuclei and the induced response was studied by bright-field microscopy. A chamber open at both sides allowing for pipette entry was prepared by affixing a glass coverslip with a few small drops of vacuum grease to the bottom of a home-built, thermostated chamber. The chamber was mounted on the microscope and filled with nuclei resuspended in physiological buffer. A temperature of 25°C was maintained using a water bath. Pipettes were pulled from glass capillaries of 1 mm diameter (World Precision Instruments, Sarasota, FL) using a pipette puller (Sutter Instruments, Novato, CA). Subsequent forging of the pipettes (Microforge MF-900, Narishige, Japan) ensured a flat pipette with a typical final diameter of 2Rp = 2.0–3.0 μm. After pulling and forging the glass capillaries, micropipettes were quickly dipped in silanization solution (Number II, dichlorodimethylsilane solution, Sigma-Aldrich, Copenhagen, Denmark) to prevent sticking of biological material to the glass surface and were thereafter incubated in an oven at 90°C for 120 min. After cooling to room temperature, pipettes were inspected on the microforger for clogging that can result from the silanization treatment. The bottom coverslip of the chamber was also silanized. Pipettes were backfilled with physiological buffer solution using a 1 mL plastic syringe fitted with a 97-mm long, 28-gauge backfiller (Microfil, World Precision Instruments, Sarasota, FL).
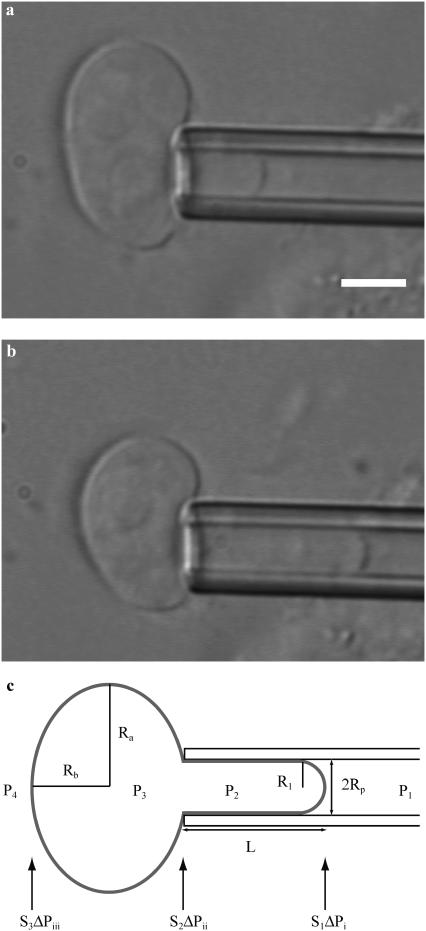
Isolated HeLa cell nuclei were visualized using bright-field optics on an inverted microscope (Zeiss Axiovert S100, Zeiss LD Achroplan 40×/0.65, Carl Zeiss, Göttingen, Germany) and images were acquired using a charge-coupled device camera (XC-85000E Donpisha, Sony, Tokyo, Japan) connected to a computer via a frame grabber (Sigma-SLC, Matrix Vision, Oppenweiler, Germany). Micromanipulators (Coherent, Ely, Cambridgeshire, UK) were used to position the micropipette that was connected to a custom-built manometer system (19,20). A pressure transducer (DP1530/N1S4A, Validyne, Northridge, CA) was used to measure the aspiration pressure (ΔP) that ranged from 1 to 7 kPa. After aspirating a nucleus, an equilibration time of 5–10 s preceded image acquisition. Thereafter the pressure was incrementally increased and at each pressure level a snapshot was acquired for analysis of nuclear geometry (Fig. 1, a and b). Additional measurements over timescales up to 300–400 s showed no significant changes in nuclear geometry. The scale factor (μm/pixel) was calibrated with a stage micrometer (Granules, Pyser-SGI, Edenbridge, UK). Image analysis was performed using ImageJ (National Institutes of Health, Bethesda, MD). The shape of a nucleus was approximated as a prolate ellipsoid with equatorial and polar radii, Ra, Rb, and Rc, where the polar radius in the axial dimension, Rc, is assumed to be equal to Rb: Ra > Rb ∼ Rc. Fig. 1 c shows the relevant geometric parameters for a nucleus under aspiration. The shape of an aspirated nucleus was approximated by a spherical endcap with a radius, R1, which is equal to the radius of the pipette, Rp; a cylinder of length L–Rp; and a prolate ellipsoid external to the pipette with radii Ra and Rb. With this approximation, the estimated volume of an unaspirated nucleus is
 |
(1) |
and under aspiration,
 |
(2) |
FIGURE 1.
Bright-field image of a nucleus isolated from a HeLa cell under aspiration at small (a) and large (b) deformations. Scale bar, 5 μm. (c) Schematic illustration depicting the relevant geometric parameters for analysis of nuclear aspiration. A projection of the nucleus (tongue) of length L formed in the pipette of radius Rp upon applying an aspiration pressure, ΔP = P1 – P4. We estimated the shape of the nucleus external to the pipette as an ellipsoid with radii Ra and Rb. In “A model for nuclear stability under micropipette aspiration”, we describe the parameters relevant for understanding ΔP: a pressure of P1 was applied through the pipette generating a pressure of P2 in the tongue projection and P3 in the bulk of the nucleus external to the pipette. The chamber pressure is P4. Pressure differences across the tip of the nuclear envelope in the tongue (ΔPi), the tongue and the inner nucleus (ΔPii), and the outer nuclear envelope (ΔPiii) are associated in the model with the filter coefficients, S1, S2, and S3 respectively.
The optically resolvable surface area was approximated as
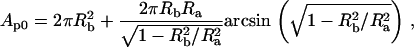 |
(3) |
and under aspiration
 |
(4) |
Extension to confocal imaged microdeformation (CIMD)
Methods for confocal imaged microdeformation (CIMD) were previously described in brief (13). Here we present a more detailed account of the experimental setup. Accommodating the confocal microscope setup for micropipette aspiration required the design of new chambers to facilitate micropipette access. Open chambers that allow for entry of the micropipette at a moderate angle were constructed by carefully using a razor blade to excise the side of a two-well chamber with a borosilicate coverslip bottom (0.17-mm thick, Nalge Nunc, Slangerup, Denmark). Isolated nuclei were visualized in this modified chamber at room temperature.
To adapt CIMD for living cells, cells were plated on coverslips (20 × 0.17 mm) (LaCon, Staig, Germany) before transfection. Before imaging, a thin layer of vacuum grease was applied to the circumference of the holder in which the coverslip was mounted. A rubber O-ring was placed on top to contain the cell medium in this open chamber into which the pipette enters at an angle. Cells were immersed in a CO2-independent medium (Minimum Essential Medium without phenol red containing 10% fetal bovine serum, 1% glutamine, 1% sodium pyruvate, 1% penicillin/streptomycin, and 1% 1M HEPES (Invitrogen, Carlsbad, CA)) and pipettes were backfilled with this medium. An objective heater (Bioptech, Butler, PA) allowed for imaging at 37°C. Buffer evaporation can result in increased salt concentrations with time and so the experimental timescale was limited to 15 min.
Micropipette aspiration was conducted as described above with the pipette mounted on a Zeiss Axiovert 200M laser scanning confocal microscope model No. 510 equipped with a META polychromatic multichannel detector and Zeiss Apochromat 40×/1.2W corr water immersion objective. The microscope, laser, and micropipette setup were mounted on an air-cushioned table that dampens vibrations, ensuring the pipette remained stationary during image acquisition. GFP was excited using the 488 nm laser line and CFP with the 458 nm laser line of an argon laser. DiIC18 and SYTOX were excited using a He-Ne laser (543 nm). Covisualization of fluorophores was performed using multitrack mode exciting GFP at 458 nm and SYTOX at 543 nm. The pinhole size was typically set to one Airy unit and the confocal slice thickness to 0.75 μm. Three-dimensional reconstructions were generated and analyzed using Zeiss LSM 510 v.3.0 software to circumvent the apparent intensity gradient in a single confocal section that can result from the non-zero angle of the micropipette in the focal plane (Fig. 2 a). Analysis of three-dimensional reconstructions allows for more accurate estimations of nuclear geometry where the polar axis of the ellipsoid in the axial dimension is now defined as Rc. Using CIMD, nuclear volume was thus estimated as
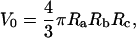 |
(5) |
and under aspiration,
 |
(6) |
FIGURE 2.
(a) Image of a three-dimensional reconstruction obtained by CIMD of an intact, living mouse embryo fibroblast (MEF) (wild-type) transiently expressing GFP-LamA. The white arrow denotes the axis of the generated intensity profile (shown in c) and yellow circles represent areas sampled in the tip of the tongue and bulk nucleus external to the pipette to construct pixel intensity histograms (shown in d) to quantify the average intensities in the tip (ρi) and bulk nucleus (ρ0). Scale bar, 5 μm. (b) Surface of revolution generated for a thin elastic shell. Based on two-dimensional nonlinear elasticity theory, we describe the variation in the density of this shell along the x axis. Rp is the pipette radius. We correlate the variation in the shell's density to the decrease in GFP-LamA intensity into the deformed tongue of the nucleus in living cells and isolated nuclei. (c) The expression derived from theory (Eq. 8) is fit to the experimentally obtained intensity profile to yield a value for a. The fit is shown in orange. (d) Pixel intensity histograms obtained for the tip of the tongue (black) and bulk nucleus (red). A simple Gaussian fit (shown in contrasting color) enables us to extract a value for the mean intensity in the tip of the tongue (ρi) and the bulk (ρ0). Taken together, ρi/ρ0 and the material parameter, a, yield a value of the area expansion to shear moduli, K/μ.
Geometric parameters were determined with 15% accuracy. All reported values are the mean value ± SD among a population of n nuclei. Each experiment was performed at least three independent times.
Characterizing fluorescence intensity profiles
Inspired by fluorescence-imaged microdeformation (21) and building on previous work (13), we determined nuclear envelope properties by analyzing the fluorescence intensity along the deformed tongue of three-dimensional reconstructions obtained by CIMD. In practice, we made two-dimensional projections of the three-dimensional reconstructions (Fig. 2 a) and constructed pixel intensity profiles toward the tip of the tongue (Fig. 2 c). Analysis of the three-dimensional reconstruction is essential as it allows us to capture the intensity changes of the fluorophore along the deformed tongue that extends through several confocal planes. Investigating the intensity distribution of single confocal slices shows that GFP-LamA was largely localized at the nuclear envelope, and was also found in the inner nucleus (Fig. 4 a). Intranuclear GFP-LamA thus contributes to the overall intensity; however, the signal from these intranuclear lamins (with the exception of bright foci) was typically weak compared to that of the nuclear envelope-associated lamins and remained constant over the experimental timescale. Hence, to a good approximation, the GFP-LamA intensity profile across a three-dimensional reconstruction reflects the intensity at the nuclear envelope.
FIGURE 4.
Nucleic acids were stained with SYTOX orange in a nucleus isolated from a HeLa cell that is transiently expressing GFP-LamA. Images (a0–c0) show a single confocal slice (0.75 μm) through the equatorial axis of an unaspirated nucleus. Images (a1–c1) are three-dimensional reconstructions generated from a stack of confocal images of the same nucleus under deformation. Shown here is one representative nucleus of n = 5. Scale bar, 5 μm.
The observed intensity profiles were interpreted using nonlinear, two-dimensional elasticity theory to obtain information about the material properties of the nuclear envelope. For a two-dimensional elastic shell deformed into a micropipette, the density, ρ, varies along the cylindrical axis of deformation, x (Fig. 2 b; see also Appendix for detailed derivation) (13),
 |
(7) |
Here Rp is the radius of the pipette and the parameter a reflects the elastic properties of the underlying material. As the fluorescence intensity is proportional to the underlying density of fluorophore (22), Eq. 7 was fit to this profile (Fig. 2 c) to yield a value of a. Together with the ratio of the relative intensities in the tip of the tongue and the bulk nucleus (unperturbed nuclear envelope external to the pipette), ρi/ρ0 (Fig. 2 d), a is related to the ratio of the area expansion (K) to shear moduli (μ) and is thus a signature of the elastic properties of the underlying material. The relationship between a and K/μ for a characteristic observed intensity ratio, ρi/ρ0 = 0.62, is shown in Fig. A1 (Appendix).
Experimentally, the ratio of the mean intensities in the tip and the bulk, ρi/ρ0, was obtained by constructing pixel intensity histograms for a circular area of the inner nucleus in the tip of the tongue and bulk nucleus (Fig. 2 a). Measurable background intensity was subtracted from the obtained pixel intensities. Pixel intensity histograms typically revealed a main peak with a relatively sharp Gaussian distribution, and an asymmetric tail extending to higher intensities containing contributions from brighter foci. In this way, heterogeneities in intensity could be separated from the mean intensities in the tip, ρi, and bulk, ρ0. The mean intensity of the bulk nucleus, ρ0, was consistent with the intensity of the unaspirated nucleus, and therefore represents the density of the unperturbed nucleus. Nonlinear regression analysis was used to obtain values for the a parameter.
RESULTS
Characterizing nuclei under micropipette aspiration
We used bright-field micropipette aspiration to determine how isolated nuclei respond to deformation. To investigate the response of specific nuclear structures, we fluorescently labeled particular components of HeLa cell nuclei, both isolated and in intact living cells, and obtained images by CIMD.
A threshold pressure is required to deform nuclei
We initially evaluated nuclear deformation by analysis of bright-field images of aspirated nuclei. When we applied a small aspiration pressure (ΔP) to isolated nuclei through the micropipette, a tight seal formed between the nucleus and micropipette. Once the pressure exceeded a threshold pressure, ΔPt, the nucleus was drawn into the micropipette, forming a small tongue with a hemispherical cap (Fig. 1 a). The threshold pressure required to aspirate an isolated nucleus was ΔPt = 510 ± 40 Pa for isolated nuclei (statistically tested population (Student's t-test) of n = 30). This threshold pressure was much greater than that required for initial deformation of Dictyostelium (∼200 Pa at the leading edge) (23) and granulocytes (∼20 Pa) (24), indicating that the surface of the nucleus is comparatively more resistant to out-of-plane deformations.
Upon further aspiration, the tongue of the nucleus inside the pipette extended within seconds (Fig. 1 b). Some creeping of the nucleus into the pipette was observed until the tongue length, L, stabilized within 5–10 s for a given pressure. In the following, we have focused on nuclei in mechanical equilibrium where the nucleus and tongue length, L, remained stable in the micropipette and did not change with time for a given aspiration pressure, ΔP. For reasons discussed below in “A model for nuclear stability under micropipette aspiration”, we characterized deformations by L/Rp.
Nuclear volume decreases during aspiration
We found that total nuclear volume decreased with each incremental increase in pressure. Both L/Rp and nuclear volume stabilized within 5–10 s after each incremental pressure increase, and also at small L/Rp, implying that nuclei were in mechanical equilibrium. Unaspirated nuclei had an estimated mean volume of 1530 ± 100 μm3 (Eqs. 1 and 2) (n = 26). During a series of incremental increases in pressure from 1 to 7 kPa, nuclei experienced a marked loss of total volume under aspiration that stabilized at 30–40% of the initial nuclear volume (Fig. 3 b, gray symbols). Three-dimensional reconstructions generated by CIMD confirmed these bright-field estimates of nuclear volume loss (Eqs. 5 and 6; Fig. 3 b, blue symbols, n = 6). A similar decrease in volume was independently confirmed by estimating the volume of three-dimensional reconstructions of nuclei in living cells subjected to micropipette aspiration (Fig. 3 b, red symbols, n = 6).
FIGURE 3.
Plot of nuclear volume, V/V0, versus aspirated tongue length, L/Rp, where the aspirated tongue length, L, is normalized with respect to the pipette radius, Rp and volumes are normalized with respect to the initial volume, V0. Plotted with gray symbols are estimates from analysis of bright-field images of isolated nuclei (n = 26). The decrease in volume with increasing aspiration pressure is exemplified by three nuclei that are plotted in solid symbols with connecting lines for visual aid. This behavior is confirmed by analysis of three-dimensional CIMD reconstructions of nuclei in and isolated from cells transiently expressing GFP-LamA. Shown here are representative isolated HeLa cell nuclei (blue symbols, n = 6) as well as nuclei in living HeLa cells (red symbols, n = 6). Different symbols represent different nuclei.
Chromatin and nucleoli remain within the aspirated nucleus
To gain insights into the behavior of the materials that remained inside the nucleus throughout this volume loss, we fluorescently labeled nucleic acids in isolated nuclei with SYTOX orange (n = 5). Nucleic acids were present throughout the aspirated nucleus and tongue and remained in the nucleus during aspiration (Fig. 4). These observations, taken together with the decrease in nuclear volume, indicate that water and small, soluble particles (e.g., salts) leave the nucleus in response to pressure, suggesting that the nuclear envelope is highly permeable to these solutes, and showing that what remains in the nucleus is a structure with reduced aqueous volume that is more resistant to deformation. To reveal more details about the physical properties of the inner nucleus, we monitored changes in nucleolar shape and position during micropipette aspiration. HeLa cells transiently expressing CFP-NLS×3 show nuclear localization of this protein with increased fluorescence intensity in the nucleoli (Fig. 5, n = 10). Under deformation of the nucleus in an intact cell (Fig. 5 b), CFP-NLS×3 remained inside the nucleus and the intensity in the deformed tongue exhibited a relatively homogeneous distribution. Nucleoli were observed to undergo slight deformation and changed in position depending on the proximity to tongue formation. Typically these subnuclear bodies remained in the ellipsoid exterior to the pipette and in some cases, depending on the initial position relative to the site of deformation, were observed to enter the tongue in the pipette and deform (not shown). These data suggest that the inner nucleus is a soft, solid-like material, and are in accordance with a previous report of confined nucleolar displacement in cells subjected to shear flow (25).
FIGURE 5.
The nucleus of a living HeLa cell that was transiently expressing CFP-NLS-NLS-NLS: (a) undeformed and (b) deformed. Shown here is one representative nucleus of n = 10. Scale bar, 5 μm.
Physical properties of the nuclear envelope
To determine the physical properties of the nuclear envelope itself, we analyzed changes in the apparent surface area of nuclei. We also compared how fluorescently labeled nuclear membranes versus lamina respond to deformation using isolated HeLa cell nuclei and CIMD. In addition, we applied the CIMD method (13) to quantitatively analyze nuclear envelope properties in intact, living MEFs lacking the nuclear envelope protein, emerin. Nuclei in emerin-deficient cells serve as a model for abnormal nuclei often found in cells from Emery-Dreifuss muscular dystrophy patients.
Nuclear surface rigidity leads to buckling and crumpling during aspiration
In nuclei isolated from HeLa cells, we found the mean estimated surface area of unaspirated nuclei to be 620 ± 30 μm2 (Eqs. 3 and 4) (n = 26). Note that this estimate of surface area does not account for the actual surface area of the nuclear envelope that may be hidden in topological variations beneath the length scale of optical resolution. With increasing tongue length, L/Rp, the total apparent surface area of nuclei decreased by ∼50–80% (Fig. 6). This decrease in the apparent surface area of nuclei during aspiration is consistent with our observations of surface crumpling of isolated nuclei under small deformations (not shown), as well as buckling of the nuclear envelope in both isolated nuclei and living cells (Figs. 1 a, 4, 7, and 8) (13). Buckling and crumpling as well as the decrease in apparent nuclear surface area may result from the substantial loss in nuclear volume and signals the shear rigidity of the nuclear envelope.
FIGURE 6.
Plot of the apparent nuclear surface area, Ap/Ap0, versus aspirated tongue length, L/Rp. Apparent surface areas were estimated from geometric analysis of bright-field images and were normalized with respect to the initial apparent area, Ap0. Shown here is data for isolated HeLa cell nuclei (n = 26). The estimated area decreases with increasing aspiration pressure as exemplified by three nuclei that are plotted in solid symbols with connecting lines for visual aid. Different symbols represent different nuclei.
FIGURE 7.
A nucleus isolated from a HeLa cell that was transiently expressing GFP-lamin A and was stained with DiIC18: (a0–c0) unaspirated; and aspirated to induce small (a1–c1) and larger (a2–c2) deformations. The white arrows in panels c0 and c2 correspond to the intensity profiles generated for projections of three-dimensional images for both unaspirated (p0) and aspirated (p2) nuclei. Here lamin intensity is shown in black and membrane intensity in red. L (gray) denotes the length of the deformed tongue of the stable lamin scaffold (see Fig. 1). Shown here is one representative nucleus of n = 11. Scale bar, 5 μm.
FIGURE 8.
Nuclei in intact, living mouse embryo fibroblasts (MEFs) transiently expressing GFP-LamA undeformed and deformed by micropipette aspiration: (a) wild-type; (b) emerin-deficient. Shown here are three-dimensional reconstructions of representative nuclei obtained by CIMD from a population of n = 5 and n = 6, respectively. Intensity analysis is performed on these projected images. Scale bar, 5 μm.
Nuclear membranes exhibit fluid-like characteristics during aspiration
Based on observations of nuclear surface rigidity, we investigated the physical characteristics of the nuclear envelope in more detail. The nuclear envelope consists of two membranes punctuated by NPCs and an underlying protein meshwork, the nuclear lamina. We previously investigated the behavior of the nuclear lamina and NPCs during aspiration (13); here, we independently analyzed the behavior of the nuclear lamina and membranes. We simultaneously imaged the GFP-LamA-labeled lamina and DiIC18-stained nuclear membranes in isolated HeLa cell nuclei using CIMD (Fig. 7, a0 and b0) (n = 11). The GFP-LamA signal revealed that the nucleus was ellipsoid in form and that the lamina was smooth and relatively homogeneous on the length scale above optical resolution (Fig. 7 a0). Upon deformation, the GFP-LamA-delineated lamina extended into the pipette (Fig. 7 a1). For relatively small deformations as pictured here, the resulting tongue projection was homogeneous in GFP-LamA intensity. Surface crumpling was also observed. With increased aspiration pressure, the tongue length, L, of the aspirated nucleus increased (Fig. 7 a2) and the GFP-LamA intensity decayed along L into the tip of the tongue (Fig. 7 p2). This intensity decay reflects that the nuclear envelope has a finite shear modulus; only solid structures can sustain such variations in density. Similar behavior was observed for NPCs (13), signaling that the lamina and NPCs form a scaffold that resists shear forces over the experimental timescale.
In contrast to this stable scaffold, nuclear membranes exhibited fluid characteristics. Nuclear membranes in unaspirated nuclei were associated with the smooth surface of the ellipsoid nucleus (Fig. 7 b0). Under deformation, membranes exhibited buckling and crumpling (Fig. 7 b1) that colocalized with GFP-LamA (Fig. 7 c1), showing that membranes were associated with the underlying lamina scaffold. The corresponding membrane intensity profile was approximately constant throughout the tongue, L (Fig. 7, c2 and p2, red), contrasting the intensity decay observed for GFP-LamA (Fig. 7, c2 and p2, black). While the lamina-NPC scaffold remained intact under deformation, nuclear membranes blebbed off the tip of the tongue in response to aspiration pressure and moved up the pipette. This is seen in the intensity profile showing fluorescence signal that extended beyond the tip of the tongue (Fig. 7, b1 and p2). Membrane blebbing was observed to occur at pressures smaller than ΔPt required for deformation of the lamina. This is consistent with the magnitude of pressure associated with out-of-plane deformations of a fluid membrane into a micropipette: 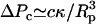 ∼ 1 Pa, where c is a prefactor of order 4–6 and κ is the membrane-bending rigidity, on the order of 10−19 J for a fluid membrane (26).
∼ 1 Pa, where c is a prefactor of order 4–6 and κ is the membrane-bending rigidity, on the order of 10−19 J for a fluid membrane (26).
An increase in aspiration pressure gave rise to a larger number of smaller, spherical blebs (Fig. 7 b2) that vesiculated at a faster rate. With time at constant pressure (5–10 s), the membrane blebs decreased in number and increased in size. Also, the vesicles no longer remained spherical but exhibited a teardrop shape until pinching off from the edge of the aspirated tongue. Together these observations indicate that blebbing vesicles were subject to aqueous shear flow (27) and that nuclear membranes have fluid characteristics.
Membrane blebbing was observed to persist with increasing aspiration pressure throughout the experimental timescale (15 min). It is important to note that membrane blebbing slowed on the 5–10 s timescale after each pressure increment but did not completely stop. The origin of these excess membranes is not clear. They may signal excess nuclear membrane area that is hidden below the optical resolution and/or a substantial reservoir (excess area) in the form of membrane-bound invaginations of the nuclear envelope that extend into the inner nucleus (28). Blebs observed in the unperturbed nucleus (Fig. 7 b0) may reflect such a membrane reservoir. Indeed, swelling of isolated nuclei demonstrates that the projected surface area can increase by at least 70% (11).
Loss of emerin alters nuclear envelope mechanics
To investigate how mutations associated with nuclear envelope diseases could affect the material properties of the nuclear envelope, we applied the CIMD method (13) to analyze large deformations in the nuclei of intact, living emerin-deficient MEFs in comparison to wild-type cells. Mutations in the gene encoding emerin, a 34-kDa protein that spans the inner nuclear membrane, are postulated to lead to increased nuclear fragility in Emery-Dreifuss muscular dystrophy.
MEFs transiently expressing GFP-LamA exhibited intensity localized at the nuclear periphery (single confocal slice, not shown) and a relatively homogeneous distribution over the surface of the nucleus (Fig. 8, a and b). Upon micropipette deformation of the intact cell, a tongue formed in the pipette and slight buckling folds were observed to radiate out from the mouth of the pipette (Fig. 8, a and b). As seen in HeLa cell nuclei, we observed that GFP-LamA intensity decreased toward the tip of the tongue, behavior characteristic of a solid shell, which signals that the nuclear envelope resists shear forces. To quantitatively describe nuclear envelope material properties in terms of the ratio of the area expansion to shear moduli, K/μ, we analyzed images of deformed nuclei in intact MEF cells and interpreted our observations in terms of nonlinear, two-dimensional elasticity theory (13). Fitting Eq. 7 to the experimentally obtained intensity profile for MEF cells yielded a larger value of the material parameter, a, for emerin-deficient compared to wild-type cells (0.44 ± 0.02 (n = 6) versus 0.21 ± 0.01 (n = 5)), reflecting a steeper decay in GFP-LamA intensity in emerin-deficient cells. Together with the ratio of the intensities in the tongue tip, ρi, and the bulk nucleus, ρ0, for each nucleus, we obtained a significantly lower value of K/μ for the emerin-deficient versus wild-type nuclear envelope (2.1 ± 0.2 versus 5.1 ± 1.3). The ratio of ρi/ρ0 was similar for both cell lines (Table 1). A ratio of K/μ > 1 shows that the in-plane shear modulus is less than the area expansion modulus, indicating that pure shear deformations are energetically more favorable. The greater than twofold reduction in K/μ for the emerin-deficient compared to wild-type cells represents a marked difference in nuclear envelope material properties. These results are summarized in Table 1.
TABLE 1.
| MEF | Wild-type | Emerin-deficient |
|---|---|---|
| A | 0.21 ± 0.01 | 0.44 ± 0.02 |
| ρi/ρ0 | 0.63 ± 0.04 | 0.62 ± 0.06 |
| K/μ | 5.1 ± 1.3 | 2.1 ± 0.2 |
| Range of L/Rp | 3.5 – 6.3 | 3.7 – 6.3 |
Values of the material parameter, a; the ratio of the intensity in the tip of the tongue to the bulk nucleus, ρi/ρ0; the ratio of the area expansion to shear moduli, K/μ; and the tongue length, L/Rp, obtained for living wild-type (n = 5) and emerin-deficient (n = 6) mouse embryo fibroblasts (MEFs). Error represents the standard deviation among a population of n nuclei.
In both emerin-deficient and wild-type MEFs, no pixels of zero intensity were typically observed in the tongue tip, indicating the absence of ruptures or tears above the length scale of optical resolution. Also, the intensity profile was stable on the experimental timescale and there was no flux or leakage of GFP-LamA across the nuclear envelope. There was no observed correlation between tongue length and genotype, as L/Rp varied from 3.5 to 6.3 for wild-type and from 3.7 to 6.3 for emerin-deficient cells. While we observed variation in L/Rp between cells, we interestingly found that ρi/ρ0 remained the same.
A model for nuclear stability under aspiration
To properly interpret deformations of nuclei using micropipette aspiration demands an understanding of the physical forces that stabilize the nucleus in the pipette during aspiration. Here we elaborate on why micropipette aspiration of nuclei cannot be interpreted using conventional methods and describe a model for nuclear stability in the pipette.
In the analysis of classical micropipette experiments (21,29–31), the fluid vesicle or cell (erythrocyte) in the pipette is treated as an elastic shell encapsulating a liquid that has constant volume under aspiration. This provides the basis for relating the pressure difference, ΔP, to the in-plane stress distribution (29). For the case of a fluid membrane, this relationship can be written simply as
 |
(8) |
where ΔP = P1 – P4 is the pressure difference between the inner pipette and chamber, σ is the surface tension, R1 is the radius of the pipette, and R2 the radius of the sphere external to the pipette. The pressure difference, ΔP, is based on the fact that the inner material is liquid; that is, the pressure in the aspirated tongue, P2, and cell body external to the pipette, P3, are equal, P2 = P3. This model requires that volume remains constant throughout the duration of the experiment. For vesicles and some cells (erythrocytes), this condition can be obtained with osmotically equivalent sugar or buffer solutions internal and external to the membrane (32). Due to volume conservation, the deformation L is uniquely related to ΔP under equilibrium conditions, and ΔP is related to surface stress, or surface tension for a fluid membrane (Eq. 8). A correction for small volume changes (∼1%) in osmotically stabilized cells and vesicles has been considered (19,32).
Our observations show that there are large volume changes (60–70%) of nuclei during micropipette aspiration. For this reason, we cannot relate ΔP to the tension in the nuclear envelope. We have thus characterized nuclear deformations in terms of L/Rp and not ΔP. As conventional micropipette analysis cannot be applied, a new model is needed to describe the stability of the nucleus under aspiration. The phenomenological model presented here is based on our experimental observations and minimal a priori assumptions. We begin by summarizing some of our key experimental observations:
First, we show that nuclear volume decreased dramatically with aspiration pressure while nucleic acids remained in the nucleus. For each incremental pressure increase, a new equilibrium volume was obtained within the 5–10 s timescale. The volume reduction upon aspiration indicates that the unaspirated inner nucleus behaves as a largely aqueous, porous material with components that can easily be exchanged with the cytoplasm. These observations suggest that chromatin and other macromolecules remained in the inner nucleus, while water and smaller solutes (e.g., salts) were exchanged with the cytoplasm. Our results are in agreement with the current knowledge of the NPC that allows for free nucleocytoplasmic exchange of molecules smaller than 8 nm (∼60 kDa) and impedes passive transport of larger molecules across the nuclear envelope (33).
Nucleoli underwent small changes in shape and position under deformation, but remained relatively fixed in position with respect to each other, suggesting that the inner nucleus has properties of a solid material.
Upon aspiration, fluid membrane blebs emerged from the nuclear envelope into the pipette. The membrane blebs had a characteristic tear-drop shape as they detached from the nuclear envelope, indicating that these blebs were subject to a gentle aqueous flow (27) through the nuclear envelope into the pipette. During a series of incremental pressure increases, the general behavior of the blebbing vesicles remained similar, suggesting that flow through the nucleus did not change significantly with increasing aspiration pressure.
Volume loss stabilized after nuclear volume was reduced by ∼60–70%. At these large volume reductions, the nucleus was resistant to further compression, preventing the complete collapse of nuclear volume and entry of the nucleus into the pipette (for Rp < Rb).
Intensity analysis revealed that the relative intensity drop of GFP-LamA between the tip and the bulk, ρi/ρ0, did not depend significantly on the degree of deformation (L), even for the same nucleus. This indicates that the nuclear envelope was stretched toward the tip region, yet was not maximally extended since the nuclear envelope at the tongue tip remained intact (no ruptures nor tears) on the length scale of optical resolution. In the case of maximal extension of the nuclear lamina meshwork in the tongue tip we would expect to see one of the hallmark signs: 1), ruptures or tears; or 2), a plateau in fluorescence into the tongue tip (34). We do not observe either sign of maximal network extension, indicating that maximal network expansion at the tip is not what limits further aspiration of the nucleus. Within the framework of the elastic model of the nuclear envelope (Appendix), this indicates that the pressure drop over the tip of the deformed tongue did not change significantly with L. Indeed, the presence and shape of the blebbing vesicles remained similar with increasing aspiration pressure, indicating that the pressure difference over the tip did not change significantly with increasing deformation. These observations suggest that the tension in the tongue tip did not change markedly during a series of incremental increases in aspiration pressure. Furthermore, there was no correlation between L/Rp for different cell types with altered nuclear envelope elasticity (Table 1).
Collectively, our data suggest that it was the extent of inner nuclear compression rather than nuclear envelope stretching that determined the degree of nuclear deformation (L/Rp) at different aspiration pressures. Our observations of relatively constant flow with increasing aspiration pressure (Observation 3) are consistent with this picture.
Here we present a new model that describes the relationship between mechanical equilibrium of the nucleus in the pipette, nuclear compression, and aqueous flow through the nucleus during aspiration. Although total nuclear volume is not conserved, a total pressure difference is maintained between the pipette and the exterior chamber. This pressure difference generates aqueous flow through the nucleus into the pipette, which we model through a series of filters that obey Darcy's law for aqueous flow. Fig. 1 c illustrates the pressures associated with the different regions of the micropipette setup, where P1 > P2 > P3 ≥ P4. We neglected the pressure difference between the bulk inner nucleus and the exterior chamber, ΔPiii = P4 – P3, since the area of the nucleus external to the pipette is relatively large and the total area of NPCs renders it highly permeable. The negligible pressure difference, ΔPiii, is further supported by the fact that the bulk nuclear envelope was not stretched significantly during aspiration.
In steady state, aqueous flow is described by Darcy's law,
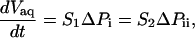 |
(9) |
where Vaq is the aqueous volume transported through the pipette and S1 and S2 are the filter coefficients with units [s × m4/kg] corresponding to flow through the nucleus. This aqueous flow is driven by the pressure difference ΔPi = P1 – P2 between the pipette and the tongue, and ΔPii = P2 – P3 between the tongue and the nucleus external to the pipette. The total aspiration pressure  can be controlled in the experiments, but neither ΔPi nor ΔPii can be quantified. However, they are related by the pressure balance,
can be controlled in the experiments, but neither ΔPi nor ΔPii can be quantified. However, they are related by the pressure balance, 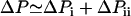 , which reflects mechanical equilibrium of the nucleus in the pipette. ΔPi and ΔPii depend on the material properties of the nuclear envelope and inner nucleus, which we do not attempt to model in detail. These pressure differences cause flow through the nucleus that is dictated by S1 and S2. The value S1 depends on NPC architecture and the number of pores in the tip. In contrast, S2 is characteristic of porous materials and changes significantly as the inner nuclear material is compressed.
, which reflects mechanical equilibrium of the nucleus in the pipette. ΔPi and ΔPii depend on the material properties of the nuclear envelope and inner nucleus, which we do not attempt to model in detail. These pressure differences cause flow through the nucleus that is dictated by S1 and S2. The value S1 depends on NPC architecture and the number of pores in the tip. In contrast, S2 is characteristic of porous materials and changes significantly as the inner nuclear material is compressed.
Based on our experimental evidence (see Observations 1–3 above) and other studies (25,35), we considered that the inner nucleus contains a loose polymeric structure with aqueous voids that are compacted during compression. Water flow at low pressure gradients through gels and porous media is well described by Darcy's law, and for compressible gels, the filter coefficient changes with compression (36). A simple dimensional analysis shows that transport is limited by the size, ξ, of the aqueous voids in the inner nucleus, 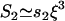 , where s2 is a kinetic prefactor. The value ξ will decrease during compression if flexible macromolecules are a major component of the inner nucleus. From models of flexible polymers in solution, such as semidilute polymer solutions or polymer gels under compression (37,38),
, where s2 is a kinetic prefactor. The value ξ will decrease during compression if flexible macromolecules are a major component of the inner nucleus. From models of flexible polymers in solution, such as semidilute polymer solutions or polymer gels under compression (37,38),  , where Π is the osmotic pressure of the inner nucleus. In the pipette setup, Π is controlled by ΔPii; thus, in a first approximation, Π(ΔPii) = Π(0) + Π′(0)ΔPii. Taking these considerations together, a relation for the pressure dependence of the filtration coefficient is
, where Π is the osmotic pressure of the inner nucleus. In the pipette setup, Π is controlled by ΔPii; thus, in a first approximation, Π(ΔPii) = Π(0) + Π′(0)ΔPii. Taking these considerations together, a relation for the pressure dependence of the filtration coefficient is
 |
(10) |
The relationship  , together with Eqs. 9 and 10, can be used to obtain the functional behavior of ΔPi and ΔPii: ΔPi saturates on s2kBT/S1Π′(0) as ΔP increases, while ΔPii grows approximately as ΔP. The total flow through the pipette does not change significantly with increasing ΔP, in agreement with the observations enumerated above. Compression of the inner nucleus also results in an overall stiffening of the nucleus that inhibits its advancement into the pipette, while the pressure over the tip changes very little, as there is no further extension of the lamina.
, together with Eqs. 9 and 10, can be used to obtain the functional behavior of ΔPi and ΔPii: ΔPi saturates on s2kBT/S1Π′(0) as ΔP increases, while ΔPii grows approximately as ΔP. The total flow through the pipette does not change significantly with increasing ΔP, in agreement with the observations enumerated above. Compression of the inner nucleus also results in an overall stiffening of the nucleus that inhibits its advancement into the pipette, while the pressure over the tip changes very little, as there is no further extension of the lamina.
DISCUSSION
Studies of nuclear mechanics are important for elucidating the structural role of specific nuclear proteins implicated in disease as well as for understanding how cells sense and respond to external forces. Micropipette deformation, in conjunction with confocal microscopy and studies of living cells, is a powerful technique for addressing such questions. However, using this technique to study nuclear mechanics demands a model for how the nucleus is stabilized during micropipette aspiration so that experimental results can be properly interpreted. In this study, we show that conventional micropipette analysis is not ideal for describing nuclear aspiration as there is loss of nuclear volume and aqueous flow through the nucleus upon aspiration. By analyzing changes in nuclear shape and the intensity distribution of different nuclear components in response to perturbation, we gain insights into the physical nature of the inner nucleus and the nuclear envelope. Here we discuss these findings in the context of our current understanding of cell nucleus mechanics.
Mechanical properties of the cell nucleus have been studied using techniques including cell compression (2,7) and strain (1,8,9), and micropipette aspiration (10–13). Some of these studies demonstrate the viscoelastic behavior of isolated nuclei (10,11). Consistent with our observations, Guilak et al. (10) found that after aspiration, chondrocyte nuclei reached equilibrium on the order of tens of seconds, while Dahl et al. (11) observed creeping behavior over hundreds of seconds for TC7 nuclei. These variations may be attributed to differences in the ratio of nuclear to pipette dimensions and/or buffer conditions. Other investigations determine a bulk modulus for the cell nucleus: Guilak et al. (10) reported a bulk nuclear modulus on the order of 1 kPa for isolated chondrocyte nuclei using micropipette aspiration; Caille et al. (7) applied uniaxial force to cells and isolated nuclei and found a bulk modulus of 5 kPa for nuclei in cells and 8 kPa for isolated nuclei. These studies reveal that the nucleus is relatively stiff compared to the cytoplasm, but do not take into account loss of nuclear volume under compression, which should be considered when estimating a bulk nuclear modulus. Here we characterized the decrease in nuclear volume upon aspiration and quantified nuclear envelope properties by analyzing nuclei in mechanical equilibrium, both isolated and in living cells.
It should be noted that many studies of nuclear mechanical stability do not address the role of the cytoskeleton. There is evidence of coupling between the nucleus and cytoskeleton (39,40), but to what extent the cytoskeleton regulates nuclear shape stability remains unclear. Investigating nuclear mechanics in both living cells and isolated nuclei is a good strategy for elucidating the role of the cytoskeleton in nuclear mechanical stability. In our experiments, we have observed the same material properties of the nuclear envelope for nuclei isolated from and in living cells (13), suggesting that cytoskeletal contributions are not an issue for characterizing the elastic properties of the nuclear envelope by CIMD.
Physical properties of the inner nucleus
Our experiments and theoretical modeling indicate that the inner nucleus is primarily aqueous and, when compressed by up to 60–70% in volume, becomes resistant to further compression. The remaining, compressed inner nuclear structure that we observe may contain condensed chromatin and/or other nuclear structures including intranuclear lamins, actin, and a ribonucleoprotein network. Such a “nuclear matrix” has been postulated to constitute an insoluble part of the inner nucleus that remains after heavy extraction of isolated nuclei (41–43) (reviewed in (44–46)). The extent to which the nuclear matrix is an artifact of the preparation procedure has been a controversial topic. Our micropipette aspiration studies show that after a series of incremental pressure increases, the remaining inner nuclear structure is highly resistant to deformation and prevents entry of the entire nucleus into the pipette. The excellent agreement between our observations of the nucleus in living cells and isolated nuclei suggests that this structure is not merely an artifact of nuclear isolation.
Consistent with our observations that the nucleus becomes more resistant to deformation with decreasing nuclear volume, a study by Hancock (47) revealed the disassembly of subnuclear compartments upon an increase in nuclear volume. These findings are all consistent with a previous report that isolated Xenopus oocyte nuclei resist compression in the presence of high concentrations of dextran (12). That study attributed the observed compressibility limit to the nuclear lamina, but compression of the bulk nucleus could also cause resistance to compression.
Nuclear envelope mechanics
Here we show that the porous, primarily aqueous inner nucleus is encapsulated by a fluid-solid composite nuclear envelope: nuclear membranes have fluid characteristics and associate with a stable, two-dimensional scaffold of lamins and NPCs that exhibits resistance to shear. We demonstrate this quantitatively using CIMD and two-dimensional elasticity theory and qualitatively with observations of surface crumpling and buckling. Surface crumpling and buckling have previously been observed in membrane systems that have finite shear moduli (48,49). This response to tension reflects that the surface bending rigidity is not sufficient to prevent out-of-plane deformation when the surface is subjected to in-plane stress (50). These observations as well as the observed intensity decay at larger deformations are consistent with the behavior of a two-dimensional solid-elastic shell. Interestingly, an intensity decay in the fluorescently labeled lamina is observed in different cell types from different species, suggesting that the solid-elastic behavior of the nuclear envelope is a universal feature of the eukaryotic cell nuclear envelope during interphase. We observed a decrease in GFP-LamA intensity into the deformed tongue in HeLa cells (derived from human cervical cancer cells) as well as in MEFs both with and without the nuclear envelope protein, emerin. Similar behavior has also been observed in GFP-Lamin-B-labeled nuclei isolated from TC7 cells (subline of African green monkey kidney epithelium cells) (11). Although nuclear envelope behavior is qualitatively similar in different nuclei, we also observe variations in nuclear envelope material properties (K/μ). Why K/μ varies among cell types is not known, but we speculate that these differences reflect cell- and tissue-specific functions.
Interplay between the nuclear envelope and the inner nucleus
The nuclear lamina is linked to both nuclear membranes and chromatin via various binding proteins (3,4), including nuclear lamins, yet the physical nature of this coupling has not been well characterized; discerning the relative contributions of the nuclear envelope and inner nucleus to nuclear mechanics is thus challenging. Our results reveal that the nuclear envelope and inner nucleus have distinctly different physical properties, and that each dominates nuclear response to small versus large deformations. We show that the nuclear envelope behaves as a two-dimensional material comprised of a solid-elastic lamina and fluidlike membranes, while the inner nucleus has characteristics of a largely aqueous, highly compressible gel. Based on our experimental observations and analytical considerations of pressure differences and fluid flow through the nucleus, our integrated understanding of nuclear behavior during microdeformation is as follows: initially at small deformations (values for L/Rp), nuclear response is governed by the behavior of the nuclear envelope, evidenced by surface buckling and crumpling. However, as nuclear volume decreases with increasing values of L/Rp during aspiration (Fig. 3), the extension of the nucleus into the pipette becomes limited by compression of the inner nucleus. As a consequence, differences in the maximal extension, L/Rp, of individual nuclei into the pipette may be attributed to variations in the initial state of inner nuclear architecture and/or nuclear volume, rather than nuclear envelope elastic properties.
To better understand the contributions of the nuclear envelope and inner nucleus to nuclear mechanics requires further experiments, yet this work remains challenging. For example, the physical properties and morphology of isolated nuclei are extremely sensitive to buffer conditions (unpublished observations) (11), suggesting that salts can induce changes in the structure (chromatin packing) (51) and mechanical properties of the inner nucleus.
Nuclear stability and disease
In this study, we applied the CIMD technique to show that emerin-deficient cells have significantly altered nuclear envelope mechanics, as the value of the area expansion to shear moduli ratio (K/μ) is less than half that of wild-type cells. This is direct evidence that loss of emerin alters nuclear envelope elastic properties. Indeed, electron microscopy studies of cells from X-EDMD patients revealed numerous nuclei with nuclear envelope fragmentation (52), and nuclear membrane breakdown in the form of chromatin-filled blebs that extrude from the nucleus (53). These structural abnormalities may be linked to altered nuclear mechanics and/or dynamics as seen by studies of nuclear shape variation and response to biaxial strain of emerin-deficient MEFs (8). Ultimately these observed changes in nuclear shape stability and nuclear envelope material properties reflect altered ultrastructure. The loss of emerin could create holes or vacancies in the lamina meshwork that alter nuclear envelope elastic properties. Emerin itself may also have a structural role in the nucleus organizing a cortical actin network at the nuclear envelope (54). As emerin is a binding partner for lamin proteins, its absence from the nuclear envelope (as in EDMD (55,56)) results in increased lamin solubility (52) and thus potentially a reduction of lamins at the nuclear envelope. It is well established that lamin A/C deficient nuclei are more susceptible to deformation by mechanical stress (1,2). Similarly, diseases of the erythrocyte membrane (e.g., hereditary ovalocytosis and elliptocytosis (26)) have been linked to changes in the connectivity of the membrane and underlying spectrin network and consequent alterations in membrane-spectrin material properties (K, μ) (57). The K/μ values for nuclei with and without emerin that we report here are important for future modeling and simulations of elastic networks to elucidate the mechanisms that govern the elasticity and lateral organization of the nuclear lamina.
How do altered nuclear envelope properties give rise to tissue-specific disease phenotypes? The observed abnormalities in nuclear envelope ultrastructure and material properties that result from, for example loss of emerin, could make nuclei less resistant to deformations in shape, leading to nuclear damage and cell death in mechanically strained tissue. Altered nuclear envelope elasticity may also affect force transmission from the cytoskeleton to the nucleus (39) as well as how forces are sensed within the nucleus, thereby modulating the response of mechanosensitive genes. In addition, emerin-mediated changes in intranuclear organization (58,59), transcriptional regulation, and gene expression (14) may also contribute to the pathological mechanism of nuclear envelope-related disease.
CONCLUSIONS
Here we characterized the material properties of the cell nucleus and present a model for the behavior of the nucleus during micropipette aspiration. Aspiration of cell nuclei is distinct from that of red blood cells and vesicles whose volume is conserved by osmotic stabilization during aspiration, and nuclear aspiration thus cannot be interpreted using conventional methods. The refined model that we present is generally applicable to any aspiration study of the cell nucleus, and more broadly to porous materials whose volume changes during aspiration. While we have shown here how the absence of a specific protein implicated in laminopathic disease (emerin) alters nuclear envelope mechanical properties, this method can be applied to a wide range of questions related to changes in nuclear structure and stability that accompany functional alterations, for example, during apoptosis (60), differentiation (59,61), and throughout the cell cycle. Such studies are critical for elucidating the pathological mechanism of nuclear envelope-related diseases as well as for developing a fundamental understanding of the mechanisms that regulate nuclear shape stability.
Acknowledgments
We are indebted to C. L. Stewart and S. Kozlov, National Cancer Institute, Bethesda, MD, for providing emerin-deficient mouse embryo fibroblasts as well as wild-type controls and to D. Shumaker and R. Goldman, Northwestern University School of Medicine, Chicago, IL, for the gift of GFP-lamin A. The Centre for Experimental Bioinformatics and the group of M. Mann, University of Southern Denmark, Denmark provided generous access to cells and cell culture facilities. J. R. Henriksen, D. H. Kim, and M. Weiss were instrumental in establishing the micropipette setup. Thanks to L. J. Foster, T. Spann, K. L. Wilson, Y. W. Lam, and J. S. Andersen for helpful discussions. Thanks also to some referees for rigorous reviewing of this manuscript.
A.C.R. was supported by a Julie Payette Scholarship from the Natural Sciences and Engineering Research Council of Canada. MEMPHYS - Centre for Biomembrane Physics is supported by the Danish National Research Foundation.
APPENDIX
Theory for the nonlinear deformation of a two-dimensional elastic shell
Our experimental results show that the nuclear envelope exhibits characteristics of a solid-elastic shell surrounding a largely aqueous inner nucleus: the decrease in the fluorescence intensity of GFP-LamA toward the tip of the deformed tongue reflects stretching of the nuclear envelope and resistance to shear. We constructed GFP-LamA intensity profiles and observed these profiles to be stable over the experimental timescale, showing that nuclear envelope components are fixed in position with respect to each other except for local deformations. Note that no ruptures or tears above the length scale of optical resolution were observed, indicating that the nuclear envelope behaves as a homogeneous, elastic material above this length scale. As the fluorescence intensity reflects the density of the underlying fluorophores, we developed an expression that describes the variation in density of a thin elastic shell under large deformation (Fig. 2), and that can be fit to our experimental intensity profiles to obtain a measure of the material's elastic properties.
Using a continuum two-dimensional approach (62), we model the nuclear envelope as a thin elastic shell constituted of elements, each of which contains components that are fixed in position with respect to each other and has a characteristic equilibrium length of l0. Under micropipette aspiration, the planar nuclear envelope is deformed into a shape represented by a cylinder and a hemispherical cap. For this surface of revolution (Fig. 2 b), the deformed elements along the meridian (x axis denoted by the white arrow) and latitude are characterized by the dimensions lm and lφ. This out-of-plane deformation is associated with the accumulation of an in-plane stress distribution and associated local lateral deformation of the surface; the stresses and strains in the plane of the nuclear envelope are thus described using a two-dimensional elastic model.
An approximate free energy per element of an isotropic, thin, hyperelastic shell is
 |
(11) |
where K and μ are the area expansion and shear moduli with units of energy per area (62,63). In the limit of small deformations,  and
and 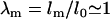 , of this model, the free energy coincides with the usual elastic free energy associated with small strains (62,64).
, of this model, the free energy coincides with the usual elastic free energy associated with small strains (62,64).
Assuming cylindrical symmetry, the local stresses along the principal directions Tm and Tφ are obtained:
 |
(12) |
We also consider mass conservation for a planar shell deformed into a revolution surface geometry,
 |
(13) |
and the condition of mechanical equilibrium (divergence-free stress tensor) (29,65),
 |
(14) |
Here s is the arc-length along the meridian and r(s) is the radius of revolution, the distance between the surface, and the axis of cylindrical symmetry. Together with some boundary conditions, these equations form a complete set of equations to specify the in-plane stress distributions and accompanying deformations associated with any three-dimensional geometric deformation of a solid plane into a surface of revolution. This description is not applicable in regions with wrinkling and buckling. Due to the nonlinear character of the model and the nontrivial surface geometry, these equations must be solved numerically with the appropriate boundary conditions. First we formulate Eqs. 12–14 in a more tractable form for analysis. Eliminating Tφ from the second of the expressions in Eq. 2 gives the form
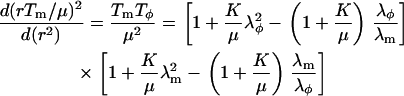 |
(15) |
For convenience, we solve the differential equations for rTm and  . Therefore we isolate λm and
. Therefore we isolate λm and  from Eq. 12,
from Eq. 12,
 |
(16) |
Combining Eqs. 13 and 16 gives the differential equation for  :
:
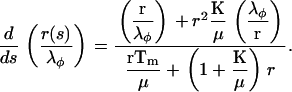 |
(17) |
Equations 15–17 show that the dependence of the material parameters K and μ on the behavior of Tm/μ and λφ appears only in the combination  . Equation 17 has the formal solution
. Equation 17 has the formal solution
 |
(18) |
Here C is given by the boundary conditions, while the solution of Eq. 15 can be obtained numerically. For the general solution, we subdivide the problem in the tip and cylindrical regions that are characterized by different geometries.
The tip region  is described by the hemispherical geometry, where
is described by the hemispherical geometry, where
 |
(19) |
and
 |
(20) |
For the boundary conditions at the pole we choose [rTm](s = 0) = 0 and  , since no rupture was observed in the tip and the deformation can be considered as isotropic. Imposing spherical geometry, Eqs. 5–7 are solved numerically up to
, since no rupture was observed in the tip and the deformation can be considered as isotropic. Imposing spherical geometry, Eqs. 5–7 are solved numerically up to  . It is interesting to note that when Eq. 10 is inserted in Eqs. 5–7, the explicit dependence on Rp drops out. Rp appears only in the combination
. It is interesting to note that when Eq. 10 is inserted in Eqs. 5–7, the explicit dependence on Rp drops out. Rp appears only in the combination  . Thus, given the initial conditions in s = 0 and
. Thus, given the initial conditions in s = 0 and  ,
,  is independent of Rp.
is independent of Rp.
The equations are easily solved in the cylindrical part  of the deformation since
of the deformation since  and Tm is a constant
and Tm is a constant  . The solution of Eq. 17 in this region is
. The solution of Eq. 17 in this region is
 |
(21) |
where  are matched with the solution from the tip region. Equations 21 and 16 make it possible to express the density profile
are matched with the solution from the tip region. Equations 21 and 16 make it possible to express the density profile
 |
(22) |
or in a short form more suitable for data fitting,
 |
(23) |
where  ,
,
 |
(24) |
and
 |
(25) |
From the form of the exponential decay parameter a in Eqs. 23 and 15–17, it is clear that a depends solely on the relative expansion in the tip λm(0) = λφ(0), and the ratio  , while
, while  in addition depends on the density of the unperturbed system, ρ0. A graph of a vs.
in addition depends on the density of the unperturbed system, ρ0. A graph of a vs.  is shown in Fig. A1.
is shown in Fig. A1.
FIGURE A1.
Theoretical plot of the material parameter, a, versus the ratio of the area expansion to the shear moduli, K/μ. The plot is generated for a ratio of the intensities in the tip to the bulk, ρi/ρ0 = 0.62.
It should be noted that the above considerations concern only the in-plane force balances associated with the deformation of an elastic shell. The corresponding force balance normal to the plane has the form
 |
(26) |
where Rm and Rφ are the principal curvature radii and ΔPs is the local pressure difference across the surface (27,65). In conventional micropipette experiments, ΔP, the pressure difference between the inner pipette and external chamber, is the sum of ΔPs over the surfaces within and exterior to the pipette. This relationship does not apply in our study.
References
- 1.Lammerding, J., P. C. Schulze, T. Takahashi, S. Kozlov, T. Sullivan, R. D. Kamm, C. L. Stewart, and R. T. Lee. 2004. Lamin A/C deficiency causes defective nuclear mechanics and mechanotransduction. J. Clin. Invest. 113:370–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Broers, J. L. V., E. A. G. Peeters, H. J. H. Kuijpers, J. Endert, C. V. C. Bouten, C. W. J. Oomens, F. P. T. Baaijens, and F. C. S. Ramaekers. 2004. Decreased mechanical stiffness in LMNA −/− cells is caused by defective nucleo-cytoskeletal integrity: implications for the development of laminopathies. Hum. Mol. Genet. 13:2567–2580. [DOI] [PubMed] [Google Scholar]
- 3.Hetzer, M. W., T. C. Walther, and I. W. Mattaj. 2005. Pushing the envelope: structure, function, and dynamics of the nuclear periphery. Annu. Rev. Cell Dev. Biol. 21:347–380. [DOI] [PubMed] [Google Scholar]
- 4.Gruenbaum, Y., A. Margalit, R. D. Goldman, D. K. Shumaker, and K. L. Wilson. 2005. The nuclear lamina comes of age. Nat. Rev. Mol. Cell Biol. 6:21–31. [DOI] [PubMed] [Google Scholar]
- 5.Muchir, A., and H. J. Worman. 2004. The nuclear envelope and human disease. Physiology (Bethesda). 19:309–314. [DOI] [PubMed] [Google Scholar]
- 6.Maraldi, N. M., S. Squarzoni, P. Sabatelli, C. Capanni, E. Mattioli, A. Ognibene, and G. Lattanzi. 2005. Laminopathies: involvement of structural nuclear proteins in the pathogenesis of an increasing number of human diseases. J. Cell. Physiol. 203:319–327. [DOI] [PubMed] [Google Scholar]
- 7.Caille, N., O. Thoumine, Y. Tardy, and J. J. Meister. 2002. Contribution of the nucleus to the mechanical properties of endothelial cells. J. Biomech. 35:177–187. [DOI] [PubMed] [Google Scholar]
- 8.Lammerding, J., J. Hsiao, P. C. Schulze, S. Kozlov, C. L. Stewart, and R. T. Lee. 2005. Abnormal nuclear shape and impaired mechanotransduction in emerin-deficient cells. J. Cell Biol. 170:781–791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Caille, N., Y. Tardy, and J. J. Meister. 1998. Assessment of strain field in endothelial cells subjected to uniaxial deformation of their substrate. Ann. Biomed. Eng. 26:409–416. [DOI] [PubMed] [Google Scholar]
- 10.Guilak, F., J. R. Tedrow, and R. Burgkart. 2000. Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Commun. 269:781–786. [DOI] [PubMed] [Google Scholar]
- 11.Dahl, K. N., A. J. Engler, J. D. Pajerowski, and D. E. Discher. 2005. Power-law rheology of isolated nuclei with deformation mapping of nuclear substructures. Biophys. J. 89:2855–2864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dahl, K. N., S. M. Kahn, K. L. Wilson, and D. E. Discher. 2004. The nuclear envelope lamina network has elasticity and a compressibility limit suggestive of a molecular shock absorber. J. Cell Sci. 117:4779–4786. [DOI] [PubMed] [Google Scholar]
- 13.Rowat, A. C., L. J. Foster, M. M. Nielsen, M. Weiss, and J. H. Ipsen. 2005. Characterization of the elastic properties of the nuclear envelope. J. Roy. Soc. Interface. 2:63–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Melcon, G., S. Kozlov, D. A. Cutler, T. Sullivan, L. Hernandez, P. Zhao, S. Mitchell, G. Nader, M. Bakay, J. N. Rottman, E. P. Hoffman, and C. L. Stewart. 2006. Loss of emerin at the nuclear envelope disrupts the Rb1/E2F and MyoD pathways during muscle regeneration. Hum. Mol. Genet. 15:637–651. [DOI] [PubMed] [Google Scholar]
- 15.Muramatsu, M., K. Smetana, and H. Busch. 1963. Quantitative aspects of isolation of nucleoli of the Walker carcinosarcoma and liver of the rat. Cancer Res. 25:693–697. [PubMed] [Google Scholar]
- 16.Jackson, D. A., J. Yuan, and P. R. Cook. 1988. A gentle method for preparing cyto- and nucleo-skeletons and associated chromatin. J. Cell Sci. 90:365–378. [DOI] [PubMed] [Google Scholar]
- 17.Moir, R. D., M. Yoon, S. Khuon, and R. D. Goldman. 2000. Nuclear lamins A and B1: different pathways of assembly during nuclear envelope formation in living cells. J. Cell Biol. 151:1155–1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fischer-Fantuzzi, L., and C. Vesco. 1988. Cell-dependent efficiency of reiterated nuclear signals in a mutant simian virus 40 oncoprotein targeted to the nucleus. Mol. Cell. Biol. 8:5495–5503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Henriksen, J. R., and J. H. Ipsen. 2004. Measurement of membrane elasticity by micro-pipette aspiration. Eur. Phys. J. E. 14:149–167. [DOI] [PubMed] [Google Scholar]
- 20.Evans, E. A., and D. Needham. 1987. Physical properties of surfactant bilayer membranes: thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 91:4219–4228. [Google Scholar]
- 21.Discher, D. E., N. Mohandas, and E. A. Evans. 1994. Molecular maps of red cell deformation: hidden elasticity and in situ connectivity. Science. 266:1032–1035. [DOI] [PubMed] [Google Scholar]
- 22.J. B. Pawley, editor. 1995. Quantitative fluorescence confocal laser scanning microscopy. In Handbook of Biological Confocal Microscopy. Plenum Press, New York. 39–53.
- 23.Merkel, R., R. Simson, D. A. Simson, M. Hohenadl, A. Boulbitch, E. Wallraf, and E. Sackmann. 2000. A micromechanical study of cell polarity and plasma membrane cell body coupling in Dictyostelium. Biophys. J. 79:707–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Evans, E., and B. Kukan. 1984. Passive material behavior of granulocytes based on large deformation and recovery after deformation tests. Blood. 64:1028–1035. [PubMed] [Google Scholar]
- 25.Tseng, Y., J. S. H. Lee, T. P. Kole, I. Jiang, and D. Wirtz. 2004. Micro-organization and visco-elasticity of the interphase nucleus revealed by particle nanotracking. J. Cell Sci. 117:2159–2167. [DOI] [PubMed] [Google Scholar]
- 26.Mohandas, N., and E. Evans. 1994. Mechanical properties of the red cell membrane in relation to molecular structure and genetic defects. Annu. Rev. Biophys. Biomol. Struct. 23:787–818. [DOI] [PubMed] [Google Scholar]
- 27.Evans, E. A., and R. S. Skalak. 1980. Mechanics and Thermodynamics of Biomembranes. CRC Press, Boca Raton, FL.
- 28.Fricker, M., M. Hollinshead, N. White, and D. Vaux. 1997. Interphase nuclei of many mammalian cell types contain deep, dynamic, tubular membrane-bound invaginations of the nuclear envelope. J. Cell Biol. 136:531–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Evans, E. A. 1980. Minimum energy analysis of membrane deformation applied to pipette aspiration and surface adhesion of red blood cells. Biophys. J. 30:265–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yeung, A., and E. Evans. 1989. Cortical shell-liquid core model for passive flow of liquid-like spherical cells into micropipettes. Biophys. J. 56:139–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Discher, D. E., and N. Mohandas. 1996. Kinematics of red cell aspiration by fluorescence-imaged microdeformation. Biophys. J. 71:1680–1694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Evans, E. A., and R. Waugh. 1977. Osmotic correction to elastic area compressibility measurements on red cell membrane. Biophys. J. 20:307–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pante, N., and U. Aebi. 1993. The nuclear pore complex. J. Cell Biol. 122:977–984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kozlov, M. M., L. V. Chernomordik, and V. S. Markin. 1990. A mechanism of formation of protein-free regions in the red cell membrane: the rupture of the membrane skeleton. J. Theor. Biol. 144:347–365. [DOI] [PubMed] [Google Scholar]
- 35.Cremer, T., K. Küpper, S. Dietzel, and S. Fakan. 2004. Higher order chromatin architecture in the cell nucleus: on the way from structure to function. Biol. Cell. 96:555–567. [DOI] [PubMed] [Google Scholar]
- 36.Yang, C., C. A. Grattoni, A. H. Muggeridge, and R. W. Zimmermann. 2002. Flow of water through channels filled with deformable polymer gels. J. Colloid Interface Sci. 250:466–470. [DOI] [PubMed] [Google Scholar]
- 37.Rubinstein, M., and R. Colby. 2003. Polymer Physics. Oxford University Press, New York.
- 38.de Gennes, P. G. 1991. Scaling Concepts in Polymer Physics. Cornell University Press, Ithaca, NY.
- 39.Maniotis, A. J., C. S. Chen, and D. E. Ingber. 1997. Demonstration of mechanical connections between integrins, cytoskeletal filaments, and nucleoplasm that stabilize nuclear structure. Proc. Natl. Acad. Sci. USA. 94:849–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Worman, H. J., and G. G. Gundersen. 2006. Here come the SUNs: a nucleocytoskeletal missing link. Trends Cell Biol. 16:67–69. [DOI] [PubMed] [Google Scholar]
- 41.Berezney, R., and D. S. Coffey. 1974. Identification of a nuclear protein matrix. Biochem. Biophys. Res. Commun. 60:1410–1417. [DOI] [PubMed] [Google Scholar]
- 42.Capco, D. G., K. M. Wan, and S. Penman. 1982. The nuclear matrix: three-dimensional architecture and protein composition. Cell. 29:847–858. [DOI] [PubMed] [Google Scholar]
- 43.Nickerson, J. A., G. Krockmalnic, K. M. Wan, and S. Penman. 1997. The nuclear matrix revealed by eluting chromatin from a cross-linked nucleus. Proc. Natl. Acad. Sci. USA. 94:4446–4450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Nickerson, J. A. 2001. Experimental observations of a nuclear matrix. J. Cell Sci. 114:463–474. [DOI] [PubMed] [Google Scholar]
- 45.Pederson, T. 1998. Thinking about a nuclear matrix. J. Mol. Biol. 277:147–159. [DOI] [PubMed] [Google Scholar]
- 46.Pederson, T. 2000. Half a century of “the nuclear matrix”. Mol. Biol. Cell. 11:799–805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hancock, R. 2004. A role for macromolecular crowding effects in the assembly and function of compartments in the nucleus. J. Struct. Biol. 146:281–290. [DOI] [PubMed] [Google Scholar]
- 48.Helfer, E., S. Harlepp, L. Bourdieu, J. Robert, F. C. MacKintosh, and D. Chatenay. 2001. Buckling of actin-coated membranes under application of a local force. Phys. Rev. Lett. 87:088103. [DOI] [PubMed] [Google Scholar]
- 49.Rowat, A. C., D. Keller, and J. H. Ipsen. 2005. Effects of farnesol on the physical properties of membranes. Biochim. Biophys. Acta. 1713:29–39. [DOI] [PubMed] [Google Scholar]
- 50.Nelson, D., T. Piran, and S. Weinberg, editors. 2004. Statistical Mechanics of Membranes and Surfaces. World Scientific Publishing, Singapore.
- 51.Bojanowski, K., and D. E. Ingber. 1998. Ionic control of chromosome architecture in living and permeabilized cells. Exp. Cell Res. 244:286–294. [DOI] [PubMed] [Google Scholar]
- 52.Markiewicz, E., R. Venables, M. Alvarez-Reyes, R. Quinlan, M. Dorobek, I. Hausmanowa-Petrucewicz, and C. Hutchison. 2002. Increased solubility of lamins and redistribution of lamin C in X-linked Emery-Dreifuss muscular dystrophy fibroblasts. J. Struct. Biol. 140:241–253. [DOI] [PubMed] [Google Scholar]
- 53.Fidziańska, A., D. Toniolo, and I. Hausmanowa-Petrusewicz. 1998. Ultrastructural abnormality of sarcolemmal nuclei in Emery-Dreifuss muscular dystrophy (EDMD). J. Neurol. Sci. 159:88–93. [DOI] [PubMed] [Google Scholar]
- 54.Holaska, J. M., A. K. Kowalski, and K. L. Wilson. 2004. Emerin caps the pointed end of actin filaments: evidence for an actin cortical network at the nuclear inner membrane. PLoS Biol. 2:1354–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ellis, J. A., M. Craxton, J. R. Yates, and J. Kendrick-Jones. 1998. Aberrant intracellular targeting and cell cycle-dependent phosphorylation of emerin contribute to the Emery-Dreifuss muscular dystrophy phenotype. J. Cell Sci. 111:781–792. [DOI] [PubMed] [Google Scholar]
- 56.Vaughan, O. A., M. Alvarez-Reyes, J. M. Bridger, J. L. V. Broers, F. C. S. Ramaekers, M. Wehnert, G. E. Morris, W. G. F. Whitfield, and C. J. Hutchison. 2001. Both emerin and lamin C depend on lamin A for localization at the nuclear envelope. J. Cell Sci. 114:2577–2590. [DOI] [PubMed] [Google Scholar]
- 57.Hansen, J. C., R. Skalak, S. Chien, and A. Hoger. 1997. Influence of network topology on the elasticity of the red blood cell membrane skeleton. Biophys. J. 72:2369–2381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Johnson, B. R., R. T. Nitta, R. L. Frock, L. Mounkes, D. A. Barbie, C. L. Stewart, E. Harlow, and B. K. Kennedy. 2005. A-type lamins regulate retinoblastoma protein function by promoting subnuclear localization and preventing proteasomal degradation. Proc. Natl. Acad. Sci. USA. 101:9677–9682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Markiewicz, E., M. Ledran, and C. J. Hutchison. 2005. Remodeling of the nuclear lamina and nucleoskeleton is required for skeletal muscle differentiation in vitro. J. Cell Sci. 118:409–420. [DOI] [PubMed] [Google Scholar]
- 60.Broers, J. L., N. M. Bronnenberg, H. J. Kuijpers, B. Schutte, C. J. Hutchison, and F. C. Ramaekers. 2002. Partial cleavage of A-type lamins concurs with their total disintegration from the nuclear lamina during apoptosis. Eur. J. Cell Biol. 81:677–691. [DOI] [PubMed] [Google Scholar]
- 61.Casolari, J. M., C. R. Brown, S. Komili, J. West, H. Hieronymus, and P. A. Silver. 2004. Genome-wide localization of the nuclear transport machinery couples transcriptional status and nuclear organization. Cell. 117:427–439. [DOI] [PubMed] [Google Scholar]
- 62.Ogden, R. W. 1984. Non-Linear Elastic Deformations. Ellis Harwood, Chichester, UK.
- 63.Stokke, B. T., A. Mikkelsen, and A. Elgsaeter. 1986. The human erythrocyte membrane skeleton may be an ionic gel. III. Micropipette aspiration of unswollen erythrocytes. J. Theor. Biol. 123:205–211. [DOI] [PubMed] [Google Scholar]
- 64.Landau, L. D., and E. M. Lifshitz. 1970. Theory of Elasticity. Course of Theoretical Physics, Vol. 7. Pergamon Press, Oxford, UK.
- 65.Flügge, W. 1973. Stresses in Shells. Springer Verlag, Heidelberg, Germany.